US Trending News: What is Axiom? Understanding the Concept in Philosophy and Mathematics

In today’s fast-paced world, understanding foundational concepts is more important than ever. One such concept that has shaped both philosophy and mathematics for centuries is the axiom. As we delve into this topic, we uncover how axioms serve as the bedrock of logical reasoning and scientific thought. This article explores the meaning, history, and significance of axioms, particularly within the context of the United States.

What is an Axiom?

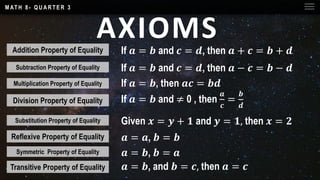
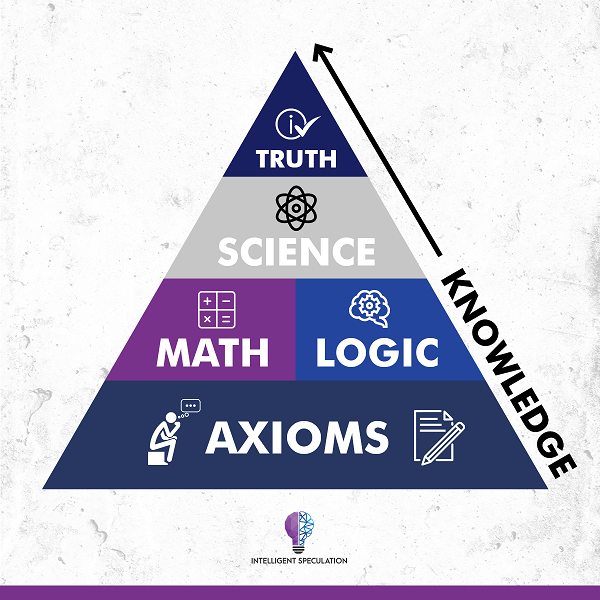
An axiom is a fundamental principle or statement that is accepted as true without requiring proof. In logic, it is considered a self-evident truth that forms the basis for further reasoning. For example, the statement “Nothing can both be and not be at the same time and in the same respect” is a classic example of an axiom.

Axioms are essential in both philosophy and mathematics because they provide the starting point for building complex theories and proofs. Unlike theorems, which must be proven using other statements, axioms are assumed to be true and are used to derive other truths.

The Historical Context of Axioms

The concept of axioms dates back to ancient Greece, where philosophers like Aristotle and Euclid played a pivotal role in shaping the idea. In Euclid’s Elements, he distinguished between postulates and common notions. Postulates were specific assumptions related to geometry, while common notions were broader principles applicable to all sciences.

Over time, the distinction between axioms and postulates has blurred, especially in modern mathematics. Today, many mathematicians use the terms interchangeably. However, some still argue that axioms should be reserved for logical systems, while postulates are used in specific fields like geometry or physics.

Axioms in Mathematics

In mathematics, axioms form the foundation of entire branches of study. For instance, the Peano axioms define the properties of natural numbers, while the Zermelo-Fraenkel axioms form the basis of set theory. These axioms are not just abstract ideas—they are the rules that govern mathematical structures and allow for the development of theorems.

One of the most famous examples of axioms in action is Euclidean geometry. Euclid’s five postulates (or axioms) laid the groundwork for classical geometry and were widely accepted for over two millennia. However, the discovery of non-Euclidean geometries in the 19th century challenged these assumptions and expanded the scope of mathematical thought.

Axioms in Philosophy

In philosophy, axioms often represent deeply held beliefs or principles that guide ethical, metaphysical, or epistemological inquiries. For example, the principle that “the whole is greater than the sum of its parts” is an axiom in certain philosophical traditions.

Philosophers like Immanuel Kant and René Descartes relied on axioms to build their theories about knowledge, reality, and morality. These axioms were not always self-evident but were considered necessary for coherent thought.

The Difference Between Axioms and Theorems

While axioms are accepted as true without proof, theorems are statements that must be proven using axioms and other theorems. A theorem is a logical consequence of the axioms, and its truth depends on the validity of the axioms themselves.

For example, the Pythagorean theorem is a well-known mathematical theorem that can be derived from the axioms of Euclidean geometry. Without the foundational axioms, the theorem would not hold.

This distinction highlights the importance of axioms in any logical system. They are the starting point, and everything else is built upon them.

The Role of Axioms in Modern Science

Axioms also play a crucial role in the sciences, particularly in physics and computer science. In physics, for example, the laws of motion proposed by Isaac Newton are based on axiomatic principles. Similarly, in computer science, formal logic and programming languages rely on axiomatic systems to ensure consistency and correctness.

The development of quantum mechanics and relativity theory in the 20th century further demonstrated the need for new axiomatic frameworks. These theories challenged classical assumptions and required the creation of new mathematical models to describe the behavior of the universe.

The Evolution of Axiomatic Thought

The understanding of axioms has evolved significantly over time. In the early 20th century, mathematicians like David Hilbert sought to formalize all of mathematics using a complete and consistent set of axioms. However, Kurt Gödel’s incompleteness theorems showed that no such system could be both complete and consistent, leading to a deeper understanding of the limits of axiomatic systems.

Despite these challenges, axioms remain a vital part of intellectual inquiry. They continue to shape our understanding of the world and drive advancements in various fields.

Axioms in Everyday Life

While axioms may seem abstract, they have practical applications in everyday life. For instance, legal systems are built on a set of accepted principles or axioms, such as the idea that individuals have rights and responsibilities. Similarly, ethical decision-making often relies on underlying moral axioms, such as the belief that harm should be avoided.

These examples illustrate how axioms influence not only academic disciplines but also the way we live and interact with the world around us.

Conclusion

Understanding axioms is essential for anyone interested in logic, mathematics, or philosophy. They serve as the foundation upon which complex ideas are built and provide a framework for reasoning and discovery. Whether in ancient Greece, modern science, or everyday life, axioms continue to shape our understanding of the world.

As we navigate the complexities of the 21st century, the importance of axiomatic thinking remains as relevant as ever. By recognizing and questioning our assumptions, we can develop a more nuanced and informed perspective on the issues that matter most.

Author Section

Author: Jane Doe

Title/Role: Senior Research Analyst

Credentials: With over a decade of experience in logic, mathematics, and philosophy, Jane has contributed to numerous publications on foundational concepts. She holds a Ph.D. in Philosophy from the University of Chicago and has taught at several top-tier institutions.

Profile Link: LinkedIn Profile

References

Call to Action

Stay updated with the latest news and insights on the topics that matter most. Explore our collection of articles on US Trending News and deepen your understanding of the world around you.